如何描述一个网络
Degree Distribution
P(k): 随机选择的节点, 度为k的的概率分布, 使用直方图来描述
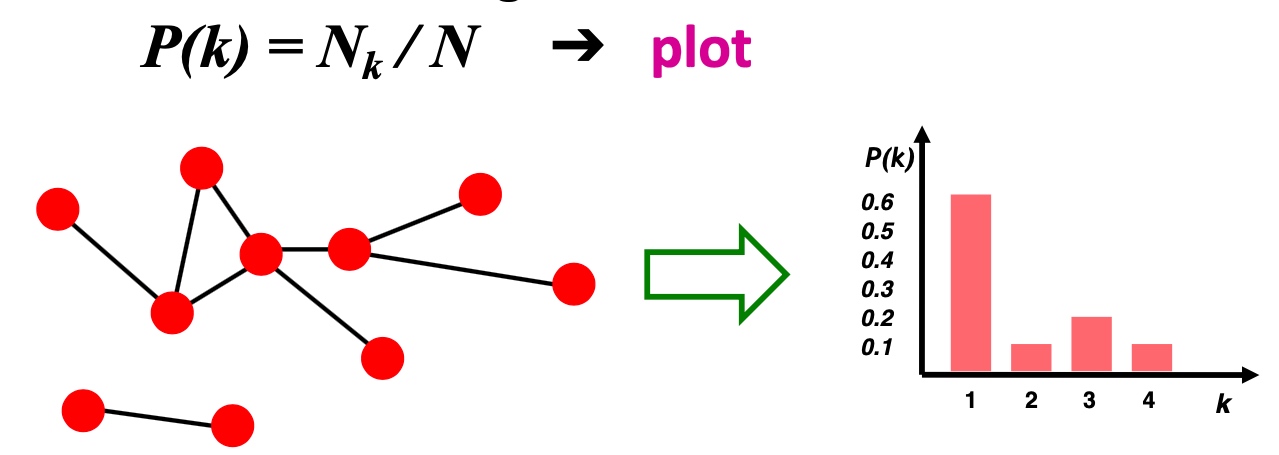
其中\(N_k\)表示度为k的节点数, 比如上图中,度为1的节点数有6, 所有节点数为10, 所以\(P(6)=0.6\)
Path Length
Path: path是指每个节点连接下一个节点的序列,其中,一个path能够重复多次相同的边, 如下图: ACBDCDEG
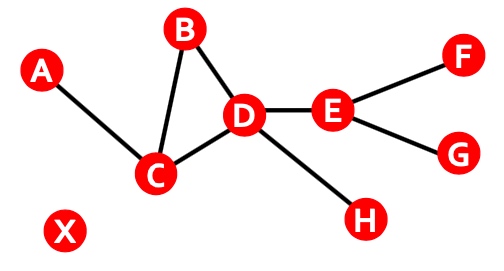
Distance: 连接节点对最少数量的边,称为两个节点间的distance,如下图,其中\(h_{B,D}=2, h_{A,X}=\infty\), 若图中两节点无连接,或中间连接断开,则distance为无穷,在有向图中,distance的计算应该考虑两个节点间的方向,如下图\(h_{B,C}=1, h{C,B}=2\),不是对称的:
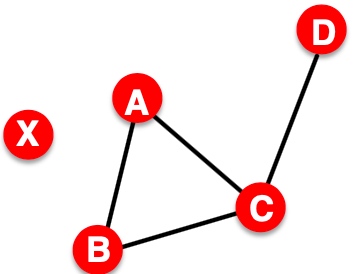
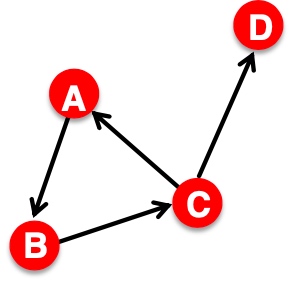
Diameter在graph中,所有节点对当中最长distance;
Average path length针对graph来说, average path length计算公式如下:
其中\(h_{ij}\)是node i到node j的distance, \(E_{max}\)是指图最多可存在的边数:\(\frac{n(n-1)}{2}\)
Cluster coefficient
cluster coefficient 对于无向图,用来描述节点i与他的邻居的链接情况, 其中节点i的度为\(k_{i}\),clustering coefficient计算公式如下:
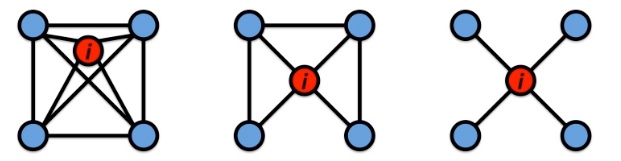
\[C_{i}=\frac{2e_{i}}{k_{i}(k_{i}-1)} \]如下图, 图的node i的cluster coefficient计算如下:\(C_{i}=\frac{2*6}{4*(4-1)}=1, C_{i}=\frac{(2*3)}{4*(4-1)}=0.5, C_{i}=\frac{2*0}{4*(4-1)}=0\)
Average clustering coefficient: \(C=\frac{1}{N}\sum_{i}^{N}C_{i}\)
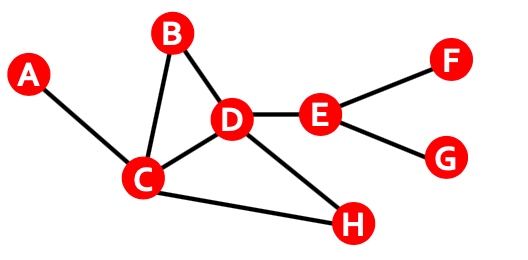
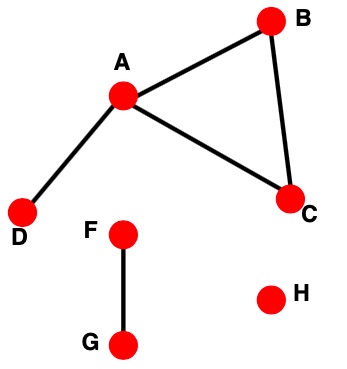
\(K_{A}=1, e_{A}=0, C_{A}=0\)
\(k_{B}=2, e_{B}=1, C_{B}=1\)
\(k_{C}=4, e_{C}=2, C_{C}=1/3\)
\(k_{D}=4, e_{D}=2, C_{D}=1/3\)
\(k_{E}=3, e_{E}=0, C_{E}=0\)
\(k_{F}=1, e_{F}=0, C_{F}=0\)
\(k_{G}=1, e_{G}=0, C_{G}=0\)
\(k_{H}=2, e_{H}=1, C_{H}=1\)
avg. clustering: C= (1+1/3+1/3+1)/8=1/3
Connected components
Connectivity
图当中最大的可连接的component:能够通过path链接的任意两个几点的最大的集合;
如何找到图当中的connect components,从图中随机节点开始,按广度优先策略遍历,标记遍历过的节点,如果,所有的节点均被遍历,那么这个未connected component, 否则从未遍历的节点中随机开始,重复广度优先策略遍历;
描述实际中的图:MSN Messenger
msn一个月的相关的数据,如下:
Degree Distribution
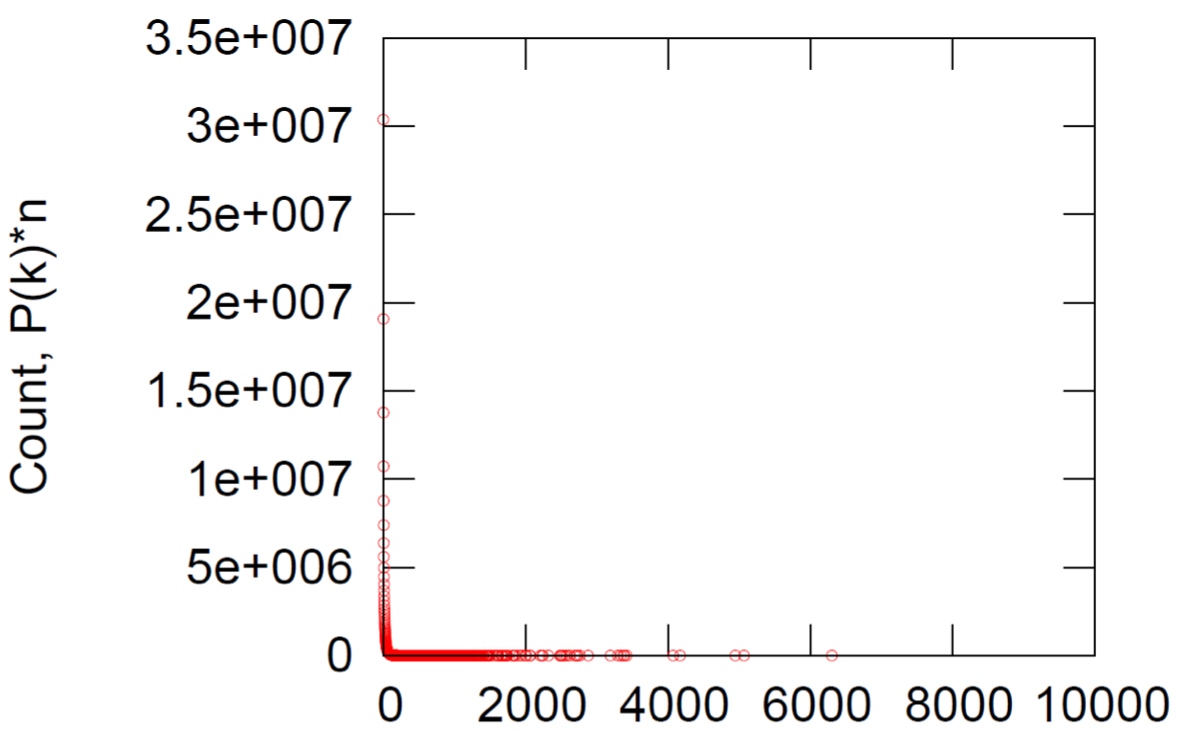
x坐标log之后:
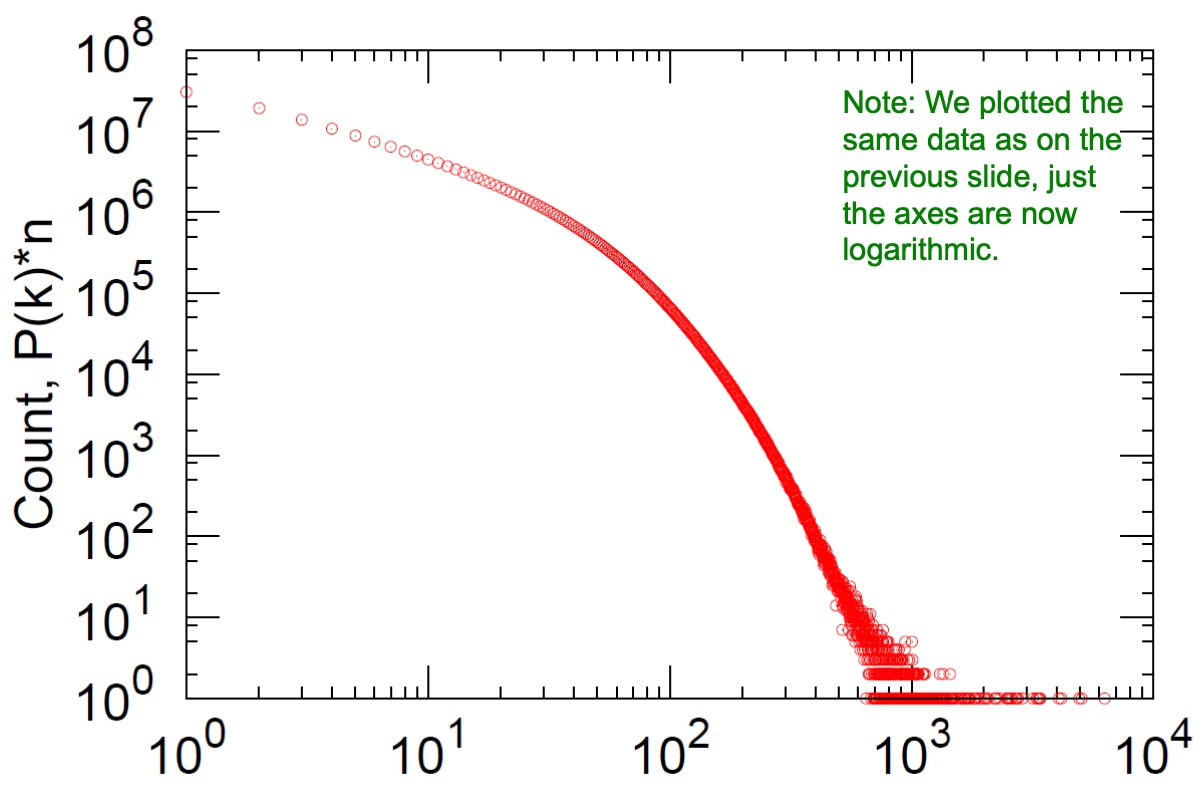
可见大部分的节点degress在个位数。
Clustering
将所有的节点的k与c绘制在如下图中,整个graph的avg culstering coefficient约为0.1140
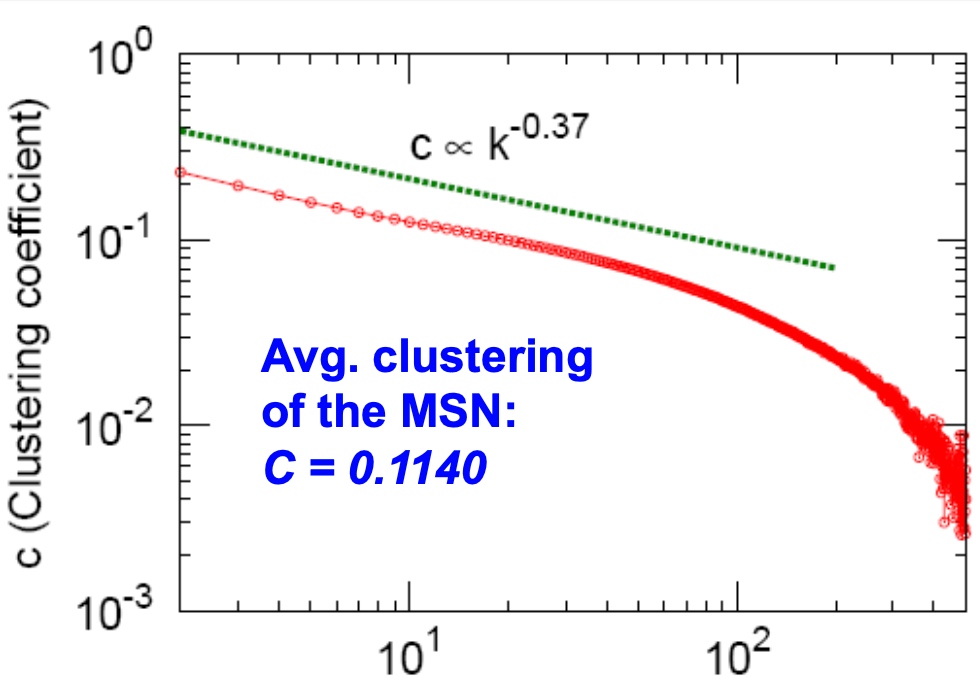
Connected Components
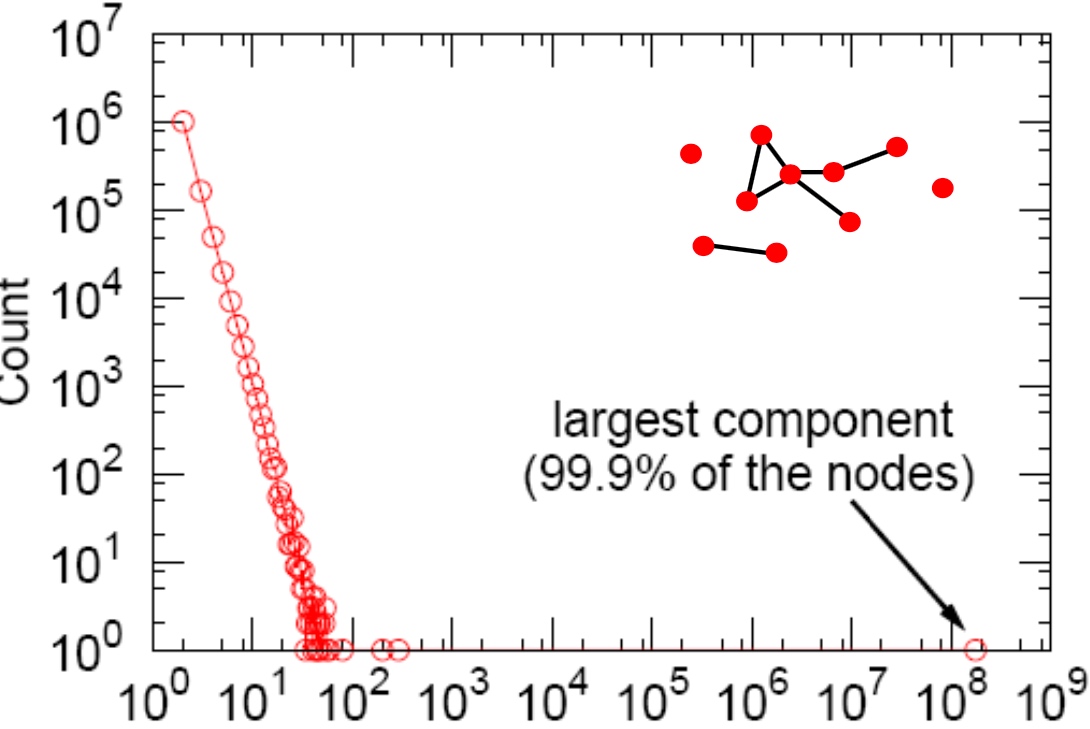
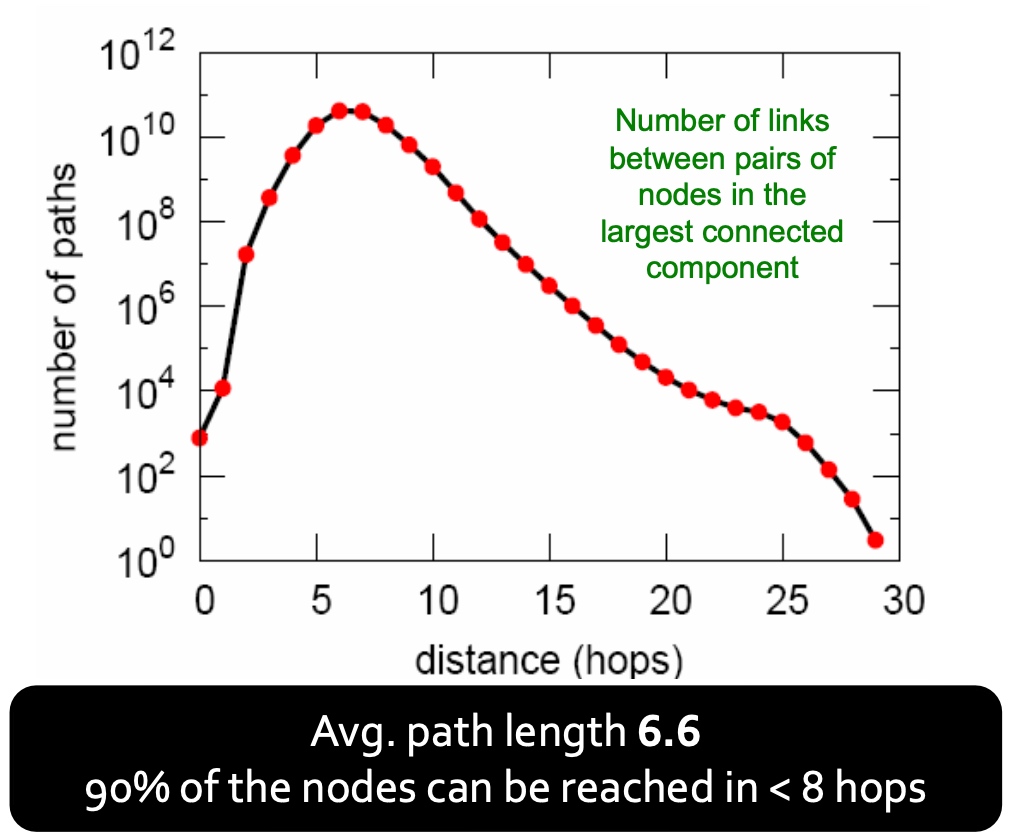
Diameter
msn的graph中平均path length为6.6, 90% 的节点能够触及在8个链接后触及到另一节点;
图的核心属性如何使用?
这些graph的属性是意外的还是在我们本身预料之中?

PPI Network
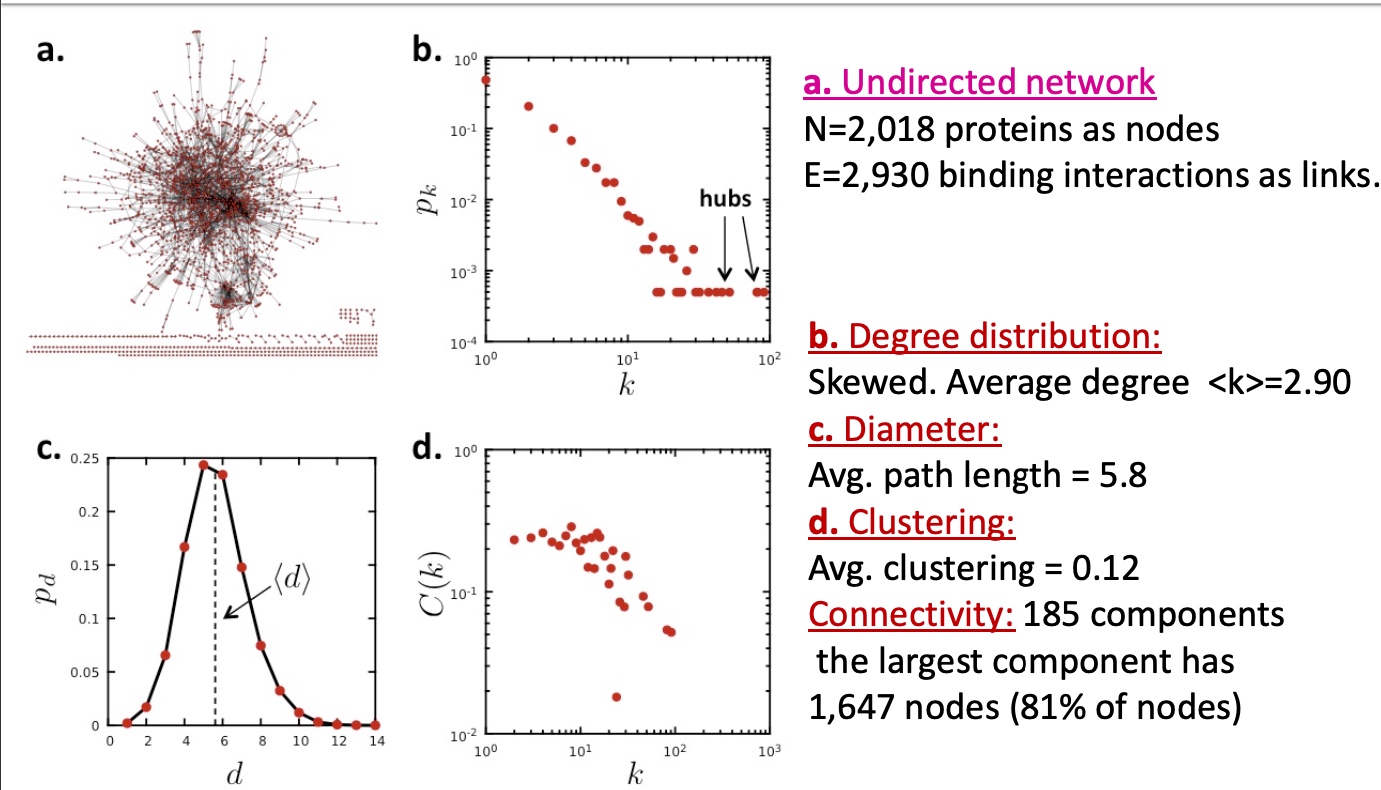
Random Graph Model
Simplest Model of Graph
ER Random Graphs
两个变种:
- \(G_{np}\): n个节点的无向图,其中每一条边是概率为p的独立同分布;
- \(G_{nm}\): n个节点的无向图,其中m个边均匀随机生成;
需要说明的是,n, p 无法唯一地的决定graph,如下图,相同的n,p下, 我们有不同的图:
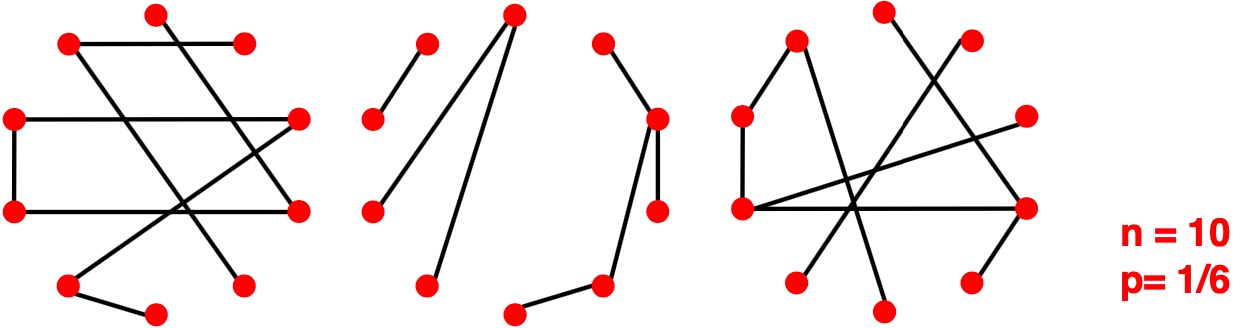
Degree Distribution of \(G_{np}\)
假定\(P{(k)}\)表示度为k在所有节点中的占比, 则
\[P_{(k)}= C_{n-1}^{k} p^{k}(1-p)^{n-1-k} \]很明显的binomial distribution, 所以均值、方差为:
\[k_mean = p(n-1) \] \[\sigma^2 = p(1-p)(n-1) \]标准差率为:\(\frac{\sigma}{k_mean} \approx \frac{1}{(n-1)^{0.5}}\),当图无限大的时候,则标准差为0, 所有的节点都为\(k_mean\)。
Clustering Coefficient of \(G_{np}\)
已知\(C_{i}=\frac{2e_{i}}{k_{i}(k_{i}-1)}\), 在\(G_{np}\),边为概率为p的独立同步分, 其中\(E[e_{i}] = p\frac{k_{i}(k_{i}-1)}{2}\), 故\(E[C_i] = \frac{pk_i(k_i - 1)}{k_i(k_i -1)} = p = \frac{k_{avg}}{n-1} \approx \frac{k_{avg}}{n}\)
Expansion
定义\(\alpha\): 如果一个graph的任意的子集S,子集中边的条数大于alpha乘以子集或者graph去除子集之后的节点数量, Expansion通常用来衡量图的lu'bang'xing:
\[\alpha = \mathop{\min}_{S \subseteqq}{\frac{\# edges\ leaving\ S} {min(|s|, |V \ S|)}} \]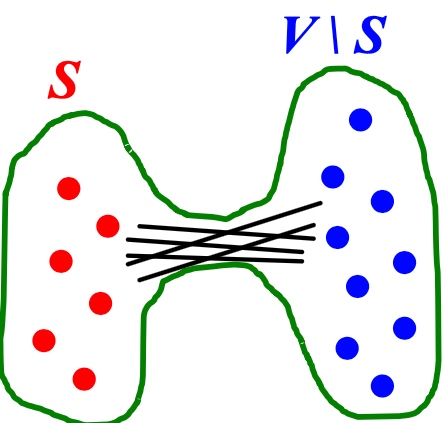
这张ppt没理解清楚,
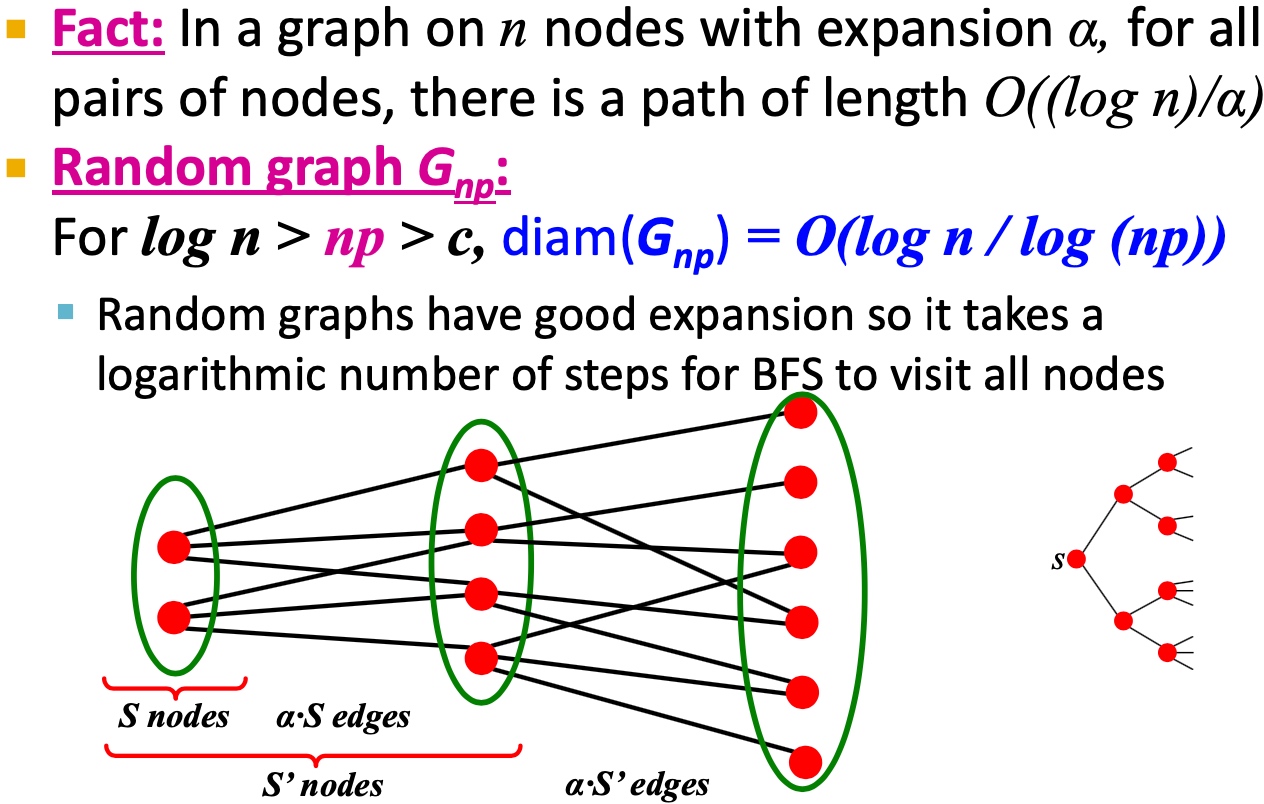
在\(G_{np}\)中,n*p为常数,所以avg deg k也为常数:
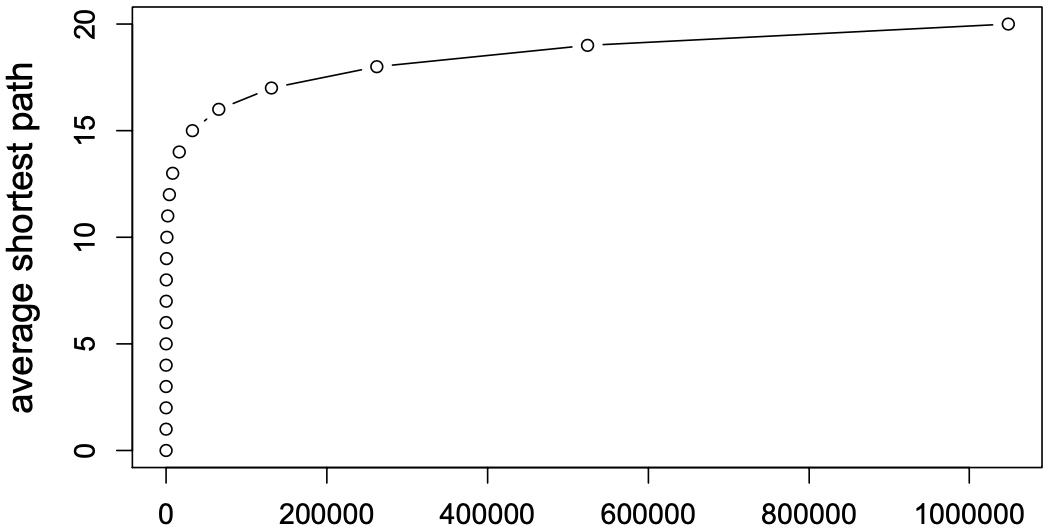
Connected Components
\(G_{np},其中n = 100000, k=p(n-1)=0.5...3\),Largest CC中节点占图中所有节点的比例
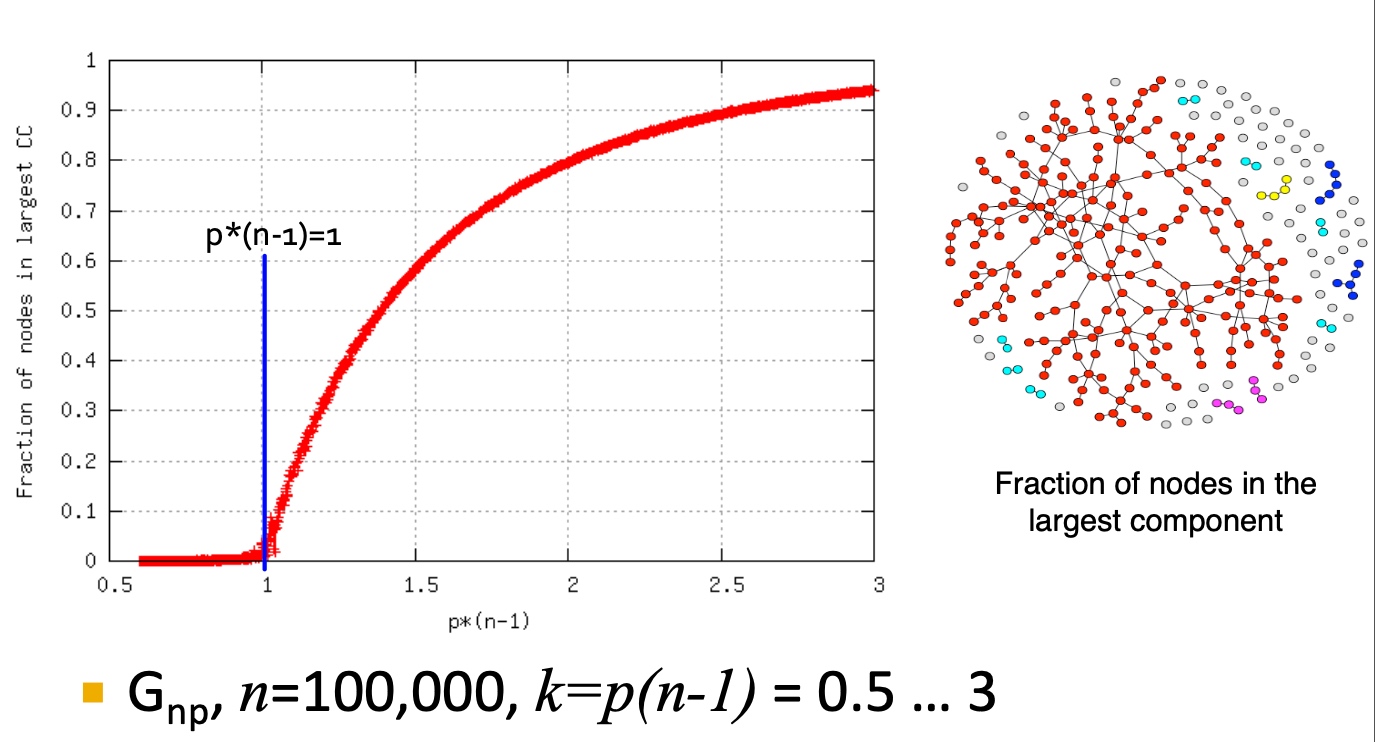
Random Graph Model vs. MSN
在Random Graph Model 和实际的MNS的4个核心属性对比:

真实网络和Random Graph类似吗 ?
- Giant Connected component: yes
- Average path length: yes
- Clustering Coefficient: No
- Degree Distribution: No
The Small-World Model--能同时保证high clustering且短path的图吗?
回顾下前面MSN network,clustering coef为0.11, 而\(G_{np}的clustering coef为8*10^{-8}\)。
另外一个例子, IMDB数据集、Electrical power grid, Network of nerons中:
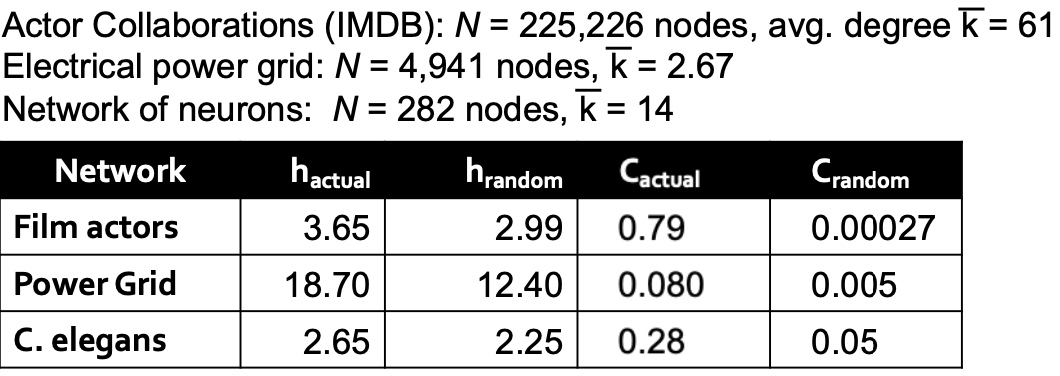
其中h:average shortest path length, C: avg clustering coefficient, random,是保证相同avg degree,相同节点下的图的情况。
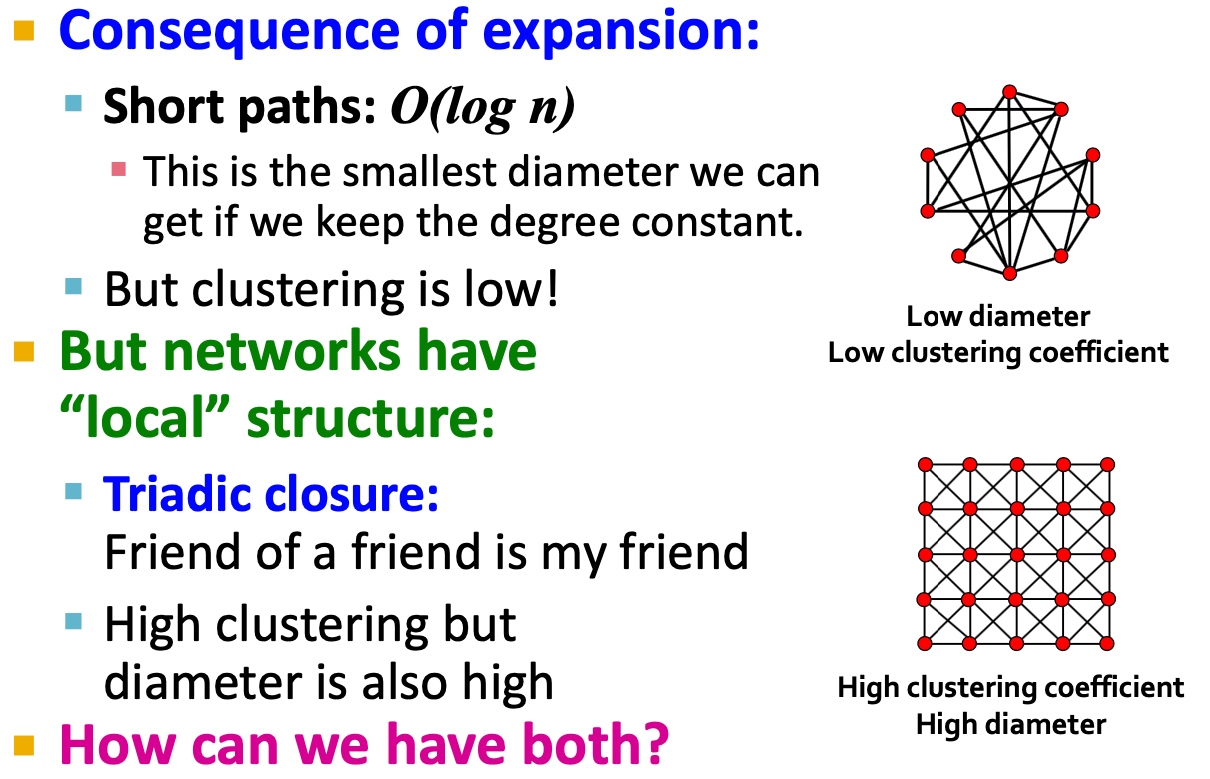
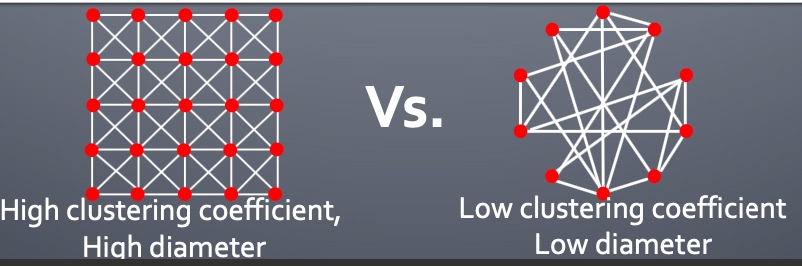
下图左边:高clustering coefficient: 朋友的朋友是我的朋友;
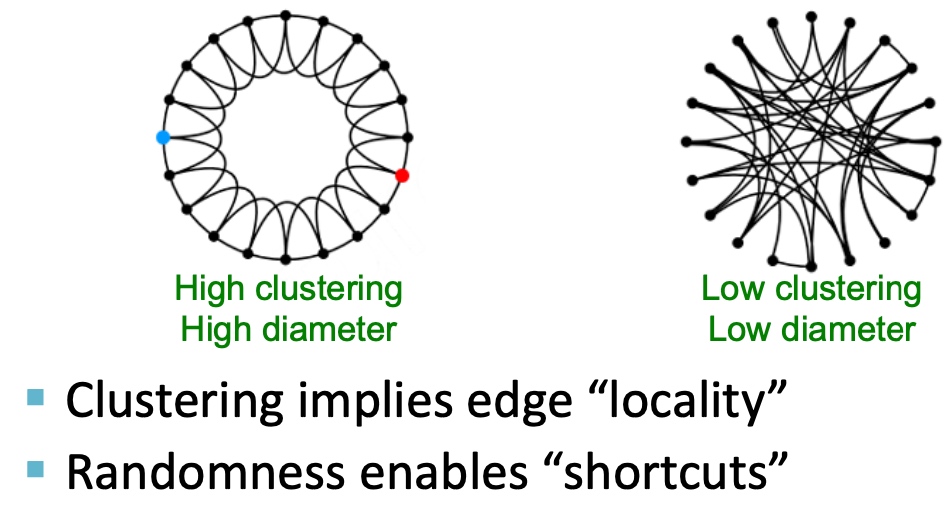
Small-World同时保证high cluster and low diameter;
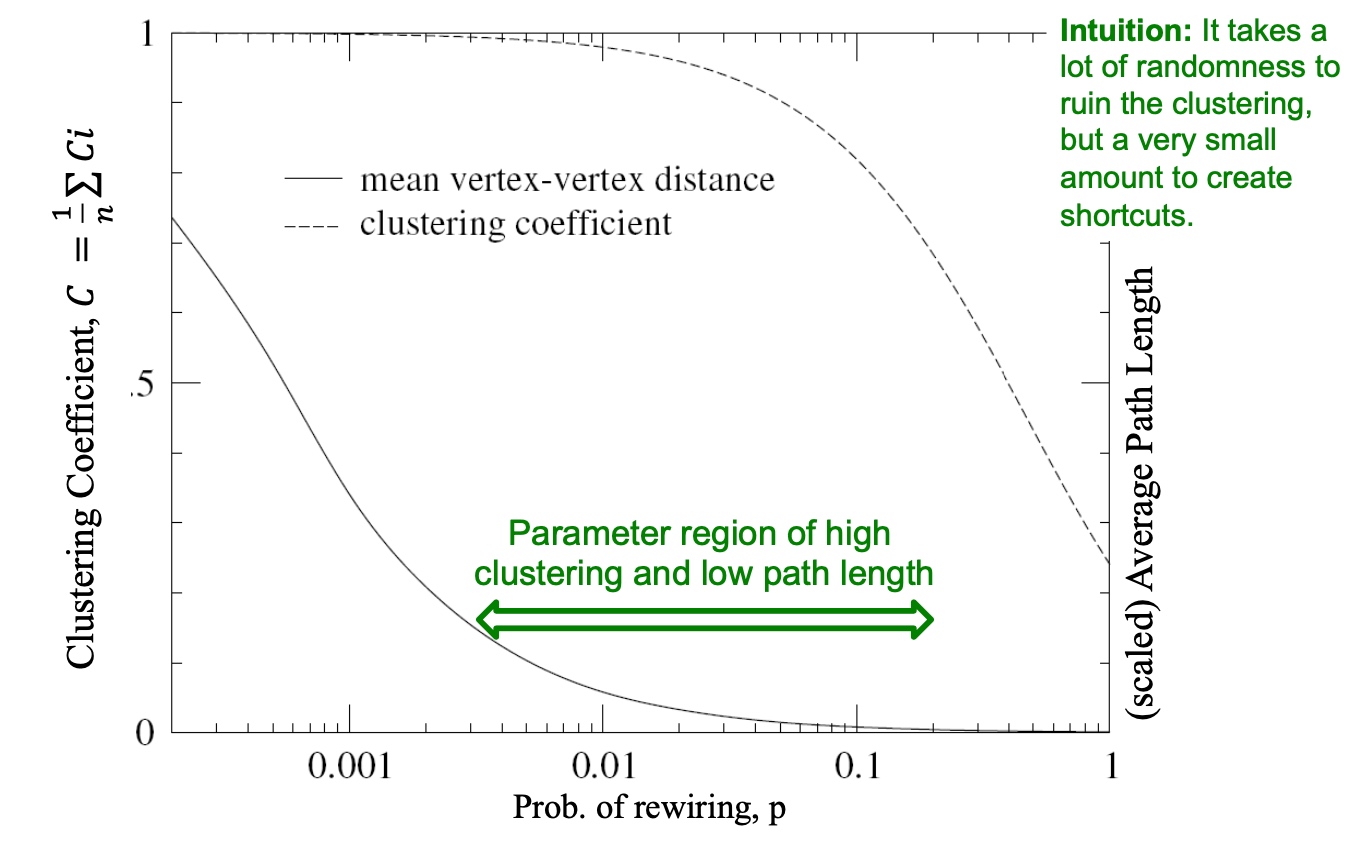
如下图,从high clustering/high diameter, 到low clustering/low diameter, 增加随机性(p变大): 即随机的将一条边的另一个端点连接到任意较远的节点上,这样可以保持high clustering,low diameter;
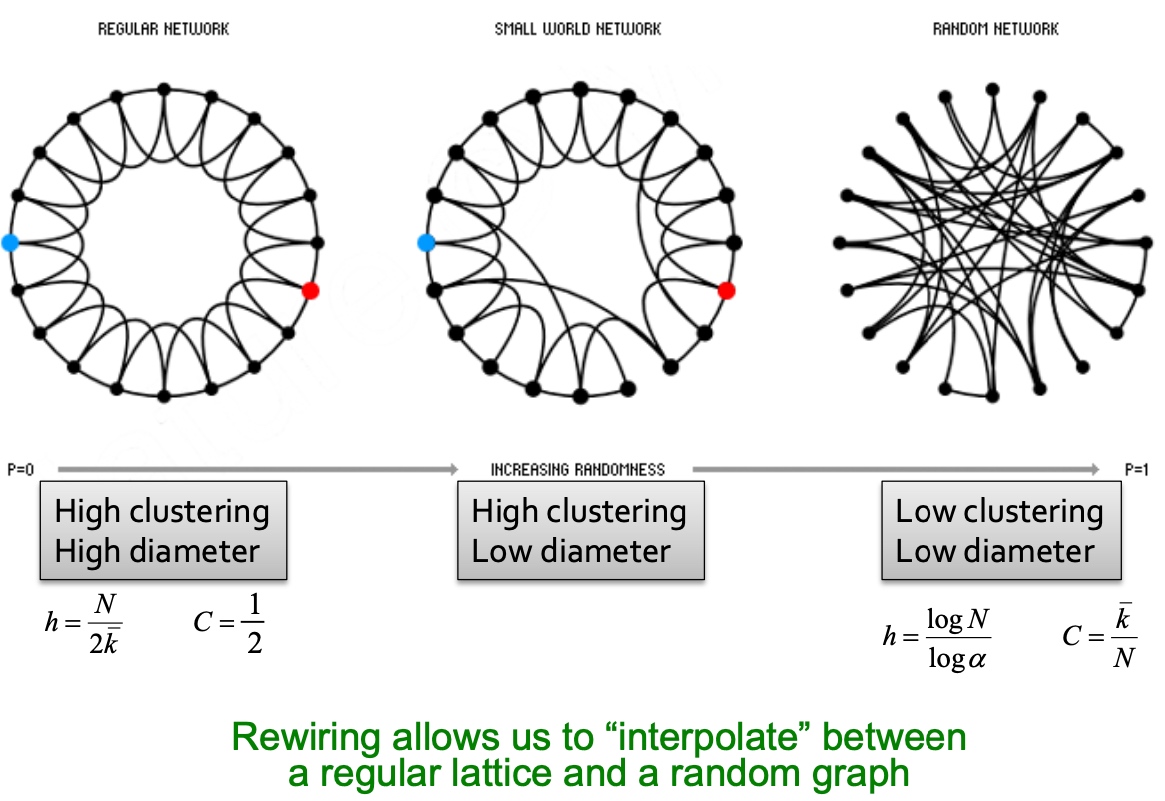
下图中的p区域保证保证high clustering 和low path length:
Kronecker Graph Model: Generating large realistic graphs
递归的graph的生成: Self-similarity
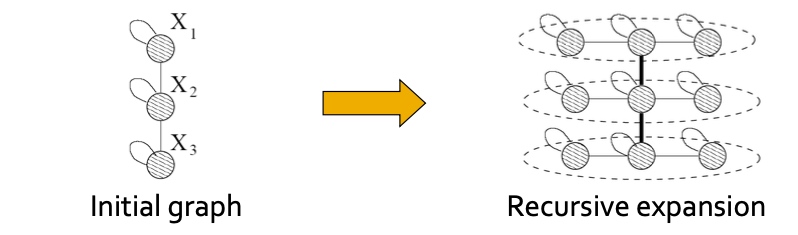
Kronecker Produce是一种生成self-similar矩阵的方法:
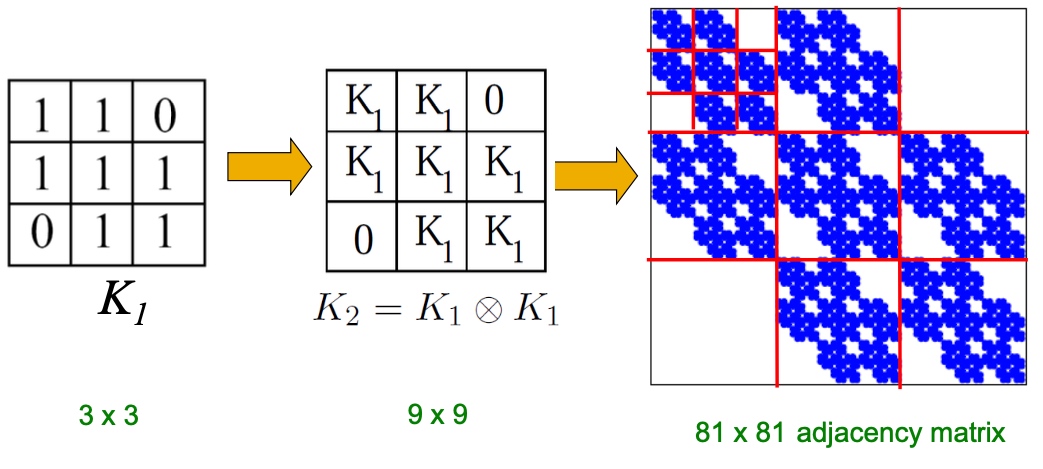
Kronecker Product 定义如下:
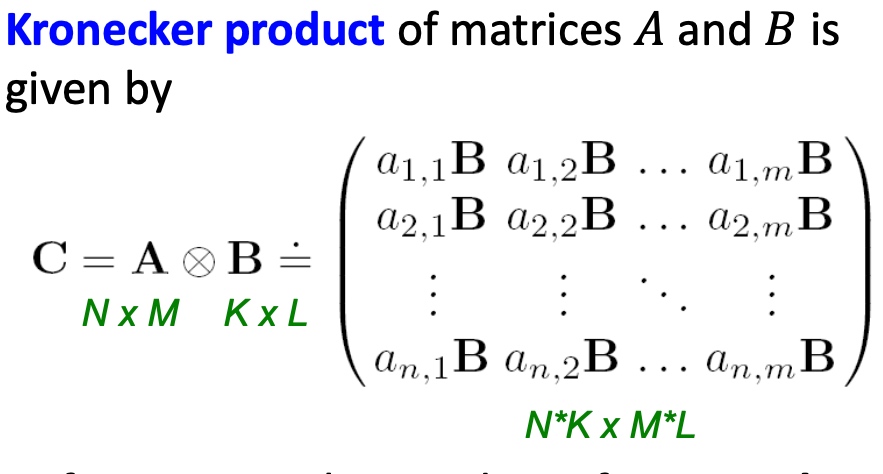
举个例子:
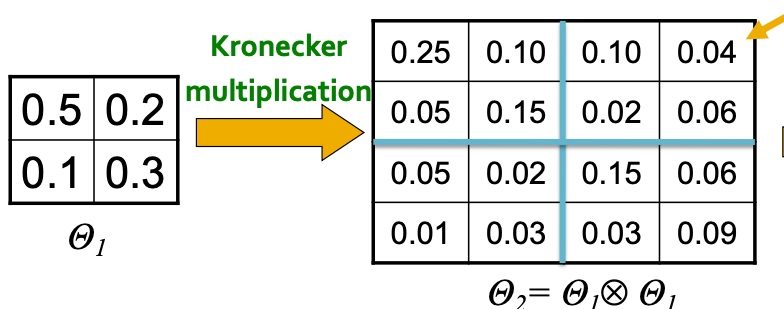
- 构建一个\(N_1 * N_1\)的初始概率矩阵;
- 计算k阶Kronecker 矩阵;
- 遍历k阶矩阵,按\(p_{uv}\)构建edge(u, v)链接

如上图最后, 需要模拟\(n^2\)次,耗时太高, 是否有更高效方法(利用其递归结构)?

真实网络与Kronecker网络很相似, 右上角为其初始矩阵:
