Granovetter's theory
马克·格兰诺维特(Mark Granovetter,1943年10月20日-),美国社会学家,斯坦福大学教授。格兰诺维特是论文被引用最多的学者之一,根据 Web of Science 的数据,社会学论文被引数排名第一和第三的文章皆出自格兰诺维特之手。格兰诺维特因为对社会网络和经济社会学的研究而成名。其最著名成就是1974年提出的弱连接理论:与自己频繁接触的亲朋好友之间是一种“强连接”,通过这种连接获取到的往往是同质性的信息;但社会上更为广泛的是一种并不深入的人际关系,这种弱关系能够使个体获得通过强关系无法获取到的信息,从而在工作和事业上、在信息的扩散上起到决定作用。
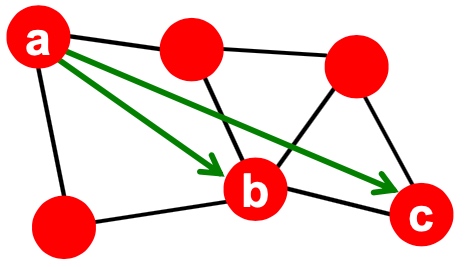
格兰诺维特的研究认为如果两个人之间有共同的朋友,那他们成为朋友的可能性较大。
格兰诺维特的研究也在真实的数据上得到了验证
Edge Overlap
简单解释下,Edge Overlap表示两个节点的邻居节点的重合程度(本身节点不在计算范围内),下图中右边部分右上图, \(N(i)=4, N(j)=4\), 去除本身i, j 所以\(N(i) \cup N(j) = 6\), \(N(i) \cap N(j) = 2\), 所以\(O_{ij}=1/3\)
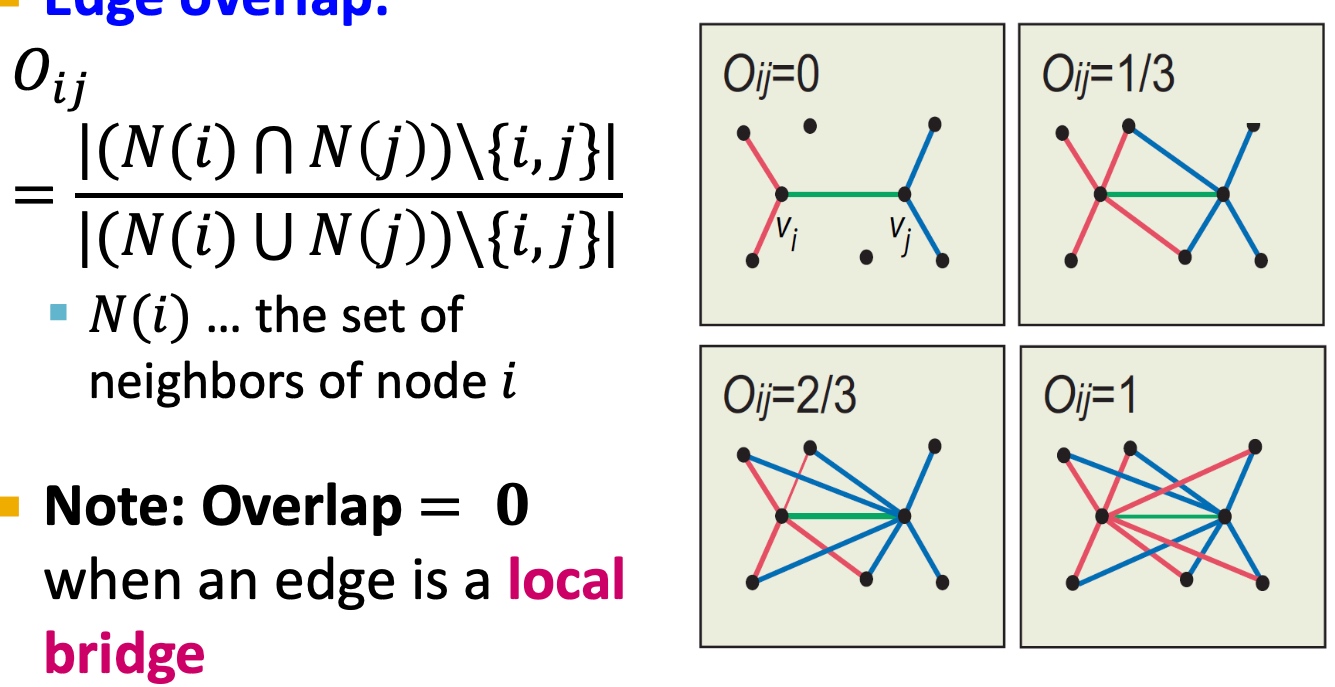
Edge Overlap被用来当做节点间链接的强弱的一种度量,通过在实际数据集(欧洲通话网络数据集得到验证), 在实际数据中,具有高边重叠的边,确实是有着强连接关系的, 这里的强连接关系即用节点间通话次数来表示关系强弱;
社区内强连接,社区间弱连接
上面的研究表明,在图中确实会存在紧密连接的社群概念,社群内的链接基本是强连接, 而社群间的连接是弱连接,强链接偏向将信息流锁紧在社群内部,而边缘连接由于涉及到多个社群之间,在信息传播上更有优势
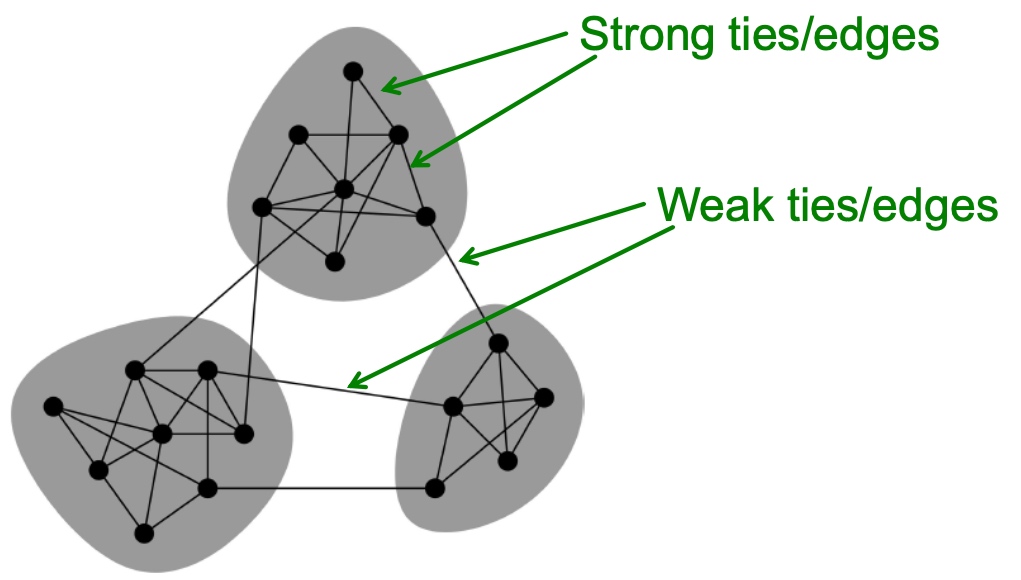
网络社群的基本概念
网络中的社群的基础定义:紧密连接的节点集合,这些节点间有较多的内部连接,而相对较少的外部连接;
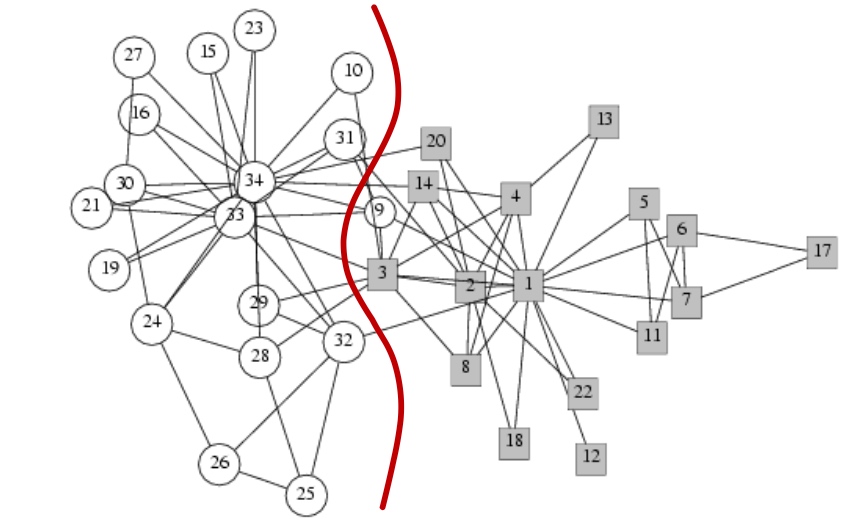
Zachary空手道俱乐部一个在图这块入门级的数据集,用来展示图网络中基本的问题如节点分类、社区发现等等;
如下图, 仅靠图的结构化关系,可以比较合理地将俱乐部进行切分,即规划至各自的社群:
另一个例子是NCAA FootBall Network:
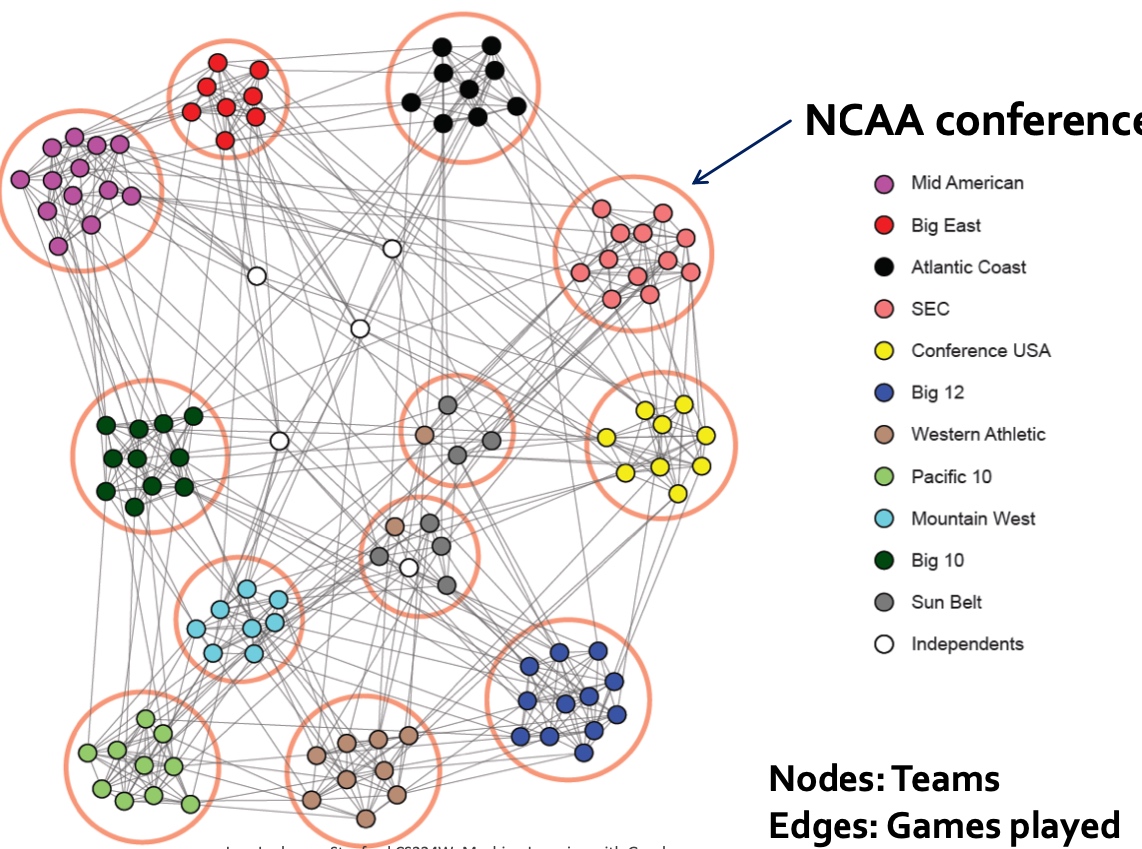
如何寻找网络中的社群?
Modularity Q用来衡量网络中社群划分的指标, 其基础含义如下:
\[Q \Rightarrow \sum_{s \in S}[(\#\ edges\ within\ group\ s) - (expected\ \#\ edges\ with\ in\ group\ s) ] \]其中\((expected\ \#\ edges\ with\ in\ group\ s)\)需要构建null model(之前的学习笔记有提到过Configuration Model, 忘记了的小伙伴可以翻一下), 保证相同的degree distribution且连接概率为均匀随机, 假定两个节点i、j,其度分别为\(k_i, k_j\),那么节点间边的期望为\(p(i,j)= \frac{k_{i}k_{j}}{2m}\),所以这个图里面所有边的期望为:
\[E_{edge}=0.5 \sum_{i \in N} \sum_{j \in N} \frac{k_{i}k_{j}}{2m}= 0.5 * \frac{1}{2m}\sum_{i \in N}k_{i}(\sum_{j \in N} k_{j})=\frac{1}{4m}* 2m*2m = m \]所以Modularity Q从:
\[Q \Rightarrow \sum_{s \in S}[(\#\ edges\ within\ group\ s) - (expected\ \#\ edges\ with\ in\ group\ s) ] \]表示为:
\[Q(G, S) = \frac{1}{2m}\sum_{s \in S}\sum_{i \in s}\sum_{j \in s}(A_{ij}-\frac{k_{i}k_{j}}{2m}) = \frac{1}{2m}\sum_{ij}[A_{ij}-\frac{k_{i}k_{j}}{2m}]\delta(c_i, c_j) \]其\(A_{ij}\ =\ 1\ if\ i->j\ 0\ otherwise, \delta(c_i, c_j)=1\ if\ c_i = c_j\ 0\ otherwise\)
Q值域为[-1, 1], 正值表示社群内的边多于期望, 当Q为0.3-0.7之间表明有显著的社群结构;
Louvain Algorithm
Louvain Algorithm是一个最大化Modularity Q的贪心算法,主要由两步构成:
过程1:Partitioning
- 初始化的时候给所有节点分配一个单独的社区;
- 针对每一个节点i,进行以下步骤:
- 计算改几点被划分到其邻居节点j所在的社群,并且计算该社群的modularity delta;
- 将节点i移入至最好modularity delta的社群;
- 迭代,直到modularity delta不再增加;
其中modularity delta \(\Delta Q\), 应该包括\(\Delta (i->C)\)(将节点i移入community C增加的Q值)与\(\Delta(D->i)\)(将节点i溢出Community D), 因为\(\\Delta(D->i)\), 在步骤1中都一样, 所以\(\Delta Q\)公式主要依赖于\(\Delta (i->C)\), 如下:
\[\Delta Q(i ->C)[\frac{\sum_{in} { k_{i, in}}}{2m} - (\frac{\sum_{tot}+k_i}{2m})^2] - [\frac{\sum_{in}}{2m} - (\frac{\sum_{tot}}{2m})^2 - (\frac{k_i}{2m})^2] \]其中:
\(\sum_{in}\) 表示社群内节点之间的边权重和(社群内边);
\(\sum_{tot}\) 表示社群中节点所有的边的边权重和(社群内边与社群外边均考虑);
\(k_{i, in}\) 表示社群中节点i与其他节点的边权重和;
\(k_i\) 表示节点i连接的所有边的权重和;
过程2: Restructuring
经过第一步之后, 会出现很多超级节点,这些超级节点间所在的社群间如果有任意的边连接,那么我们要连接超级节点, 超级节点间的边的权重等于他们相应地社群间所有边权重的和;
具体的伪代码如图,逻辑还是相对比较简单的:

回顾与真实数据展示
每一个pass 包含:partitioning和restructuring 两个部分, 如下,迭代直到收敛:
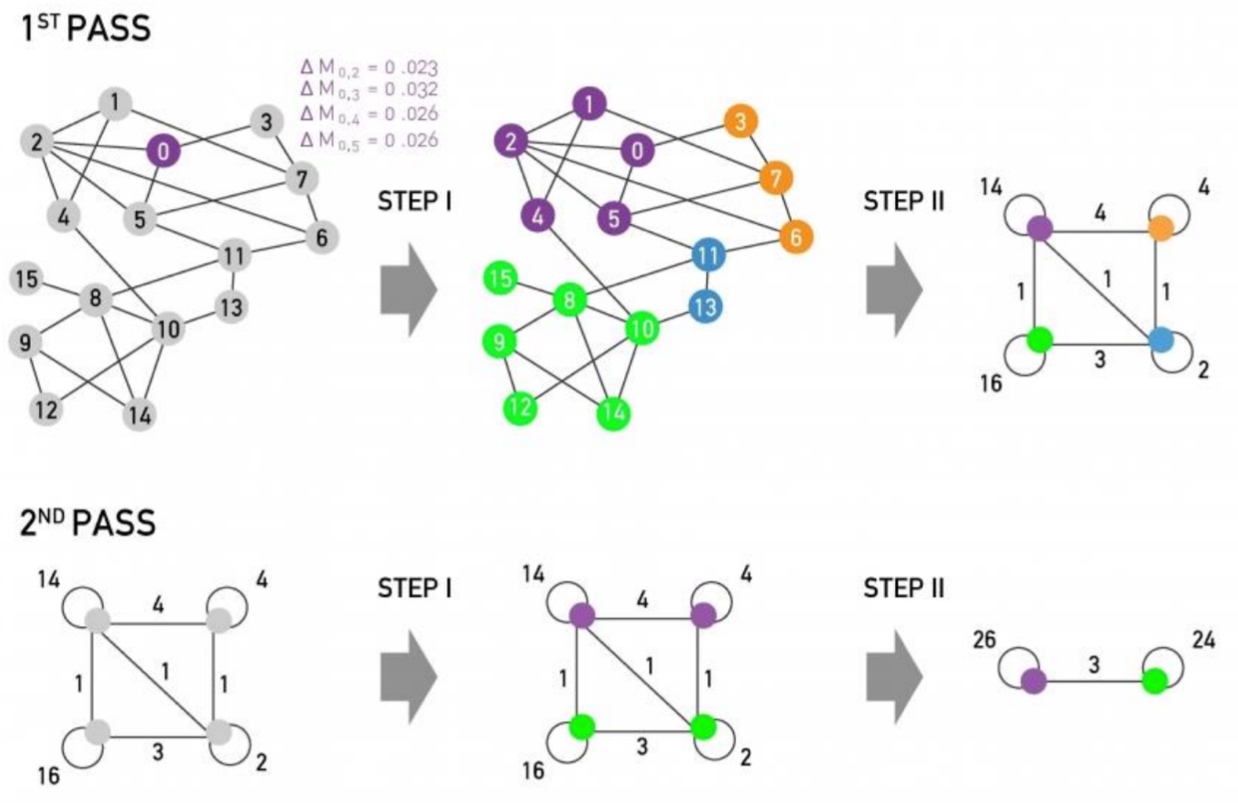
真实数据集上的一个例子:
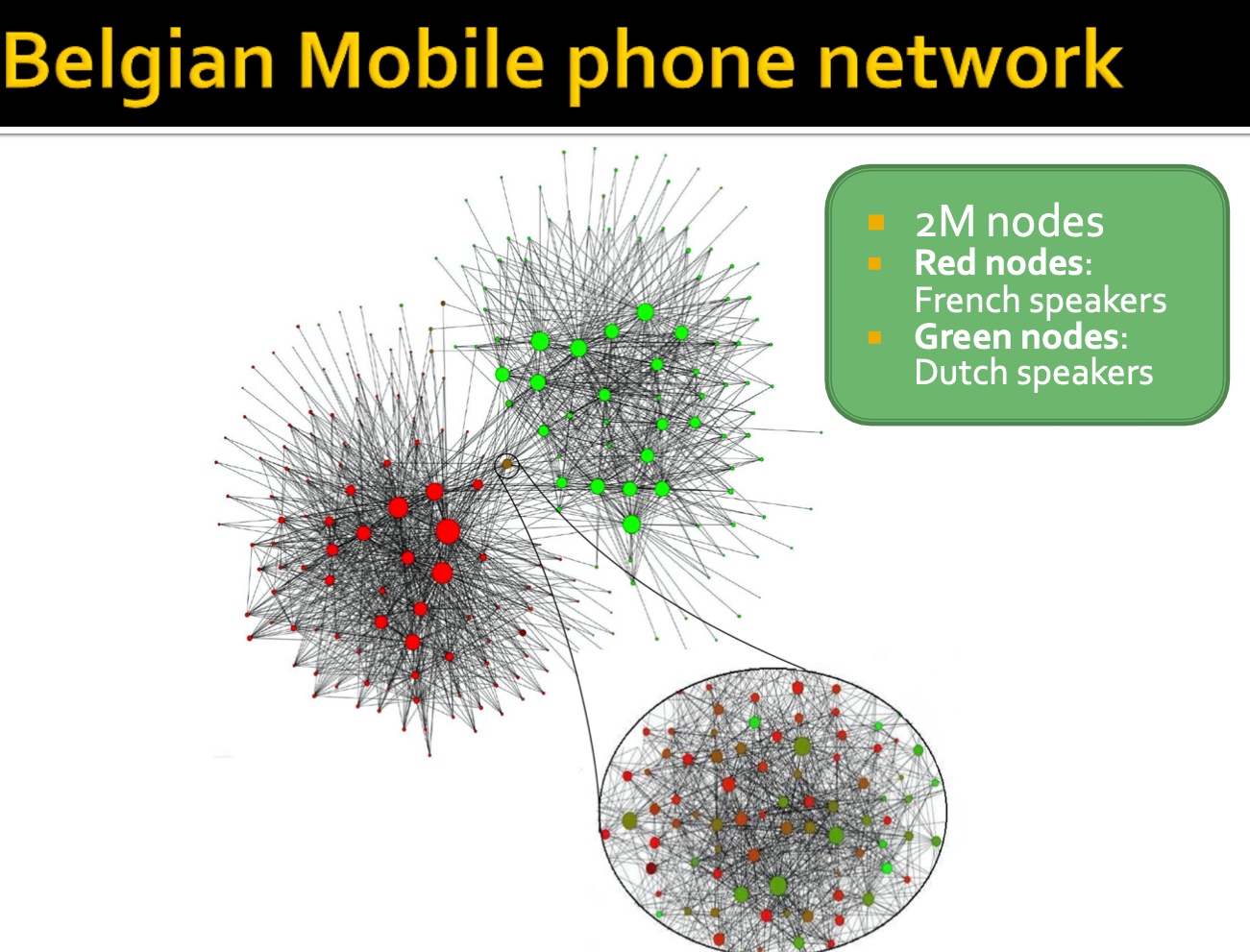
检测有重叠的社群算法:BigCLAM
何谓有重叠的社群?
无重叠的社群与有重叠的社群
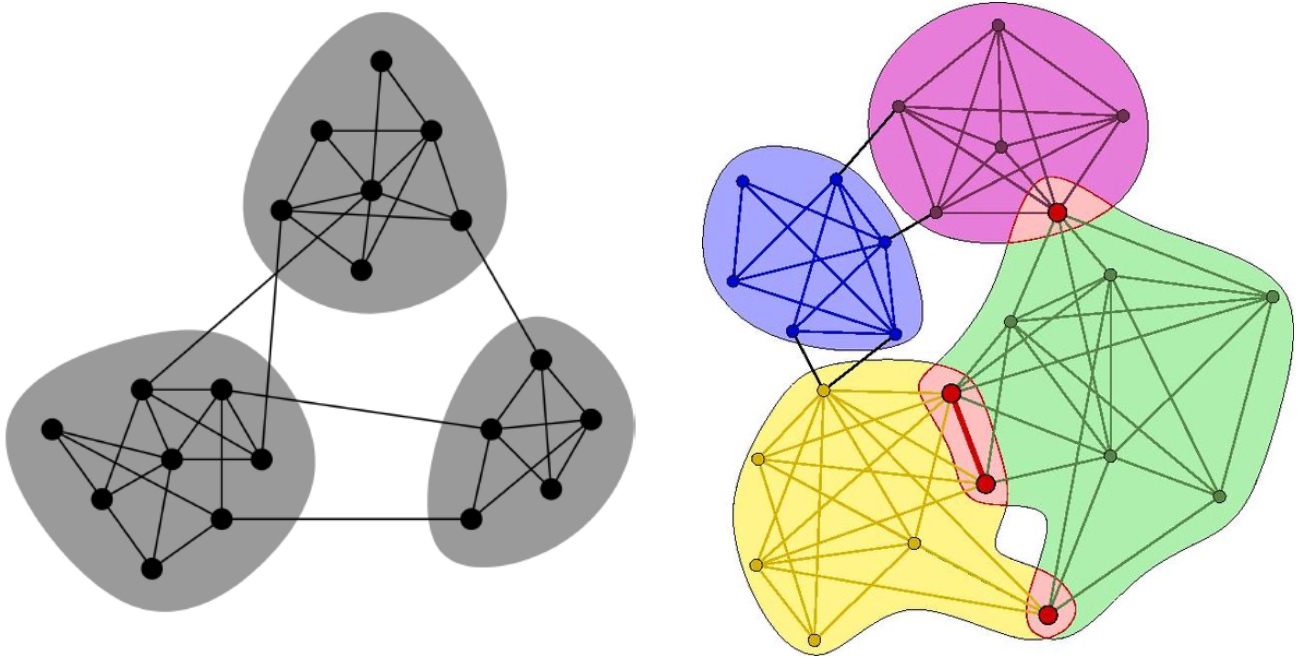
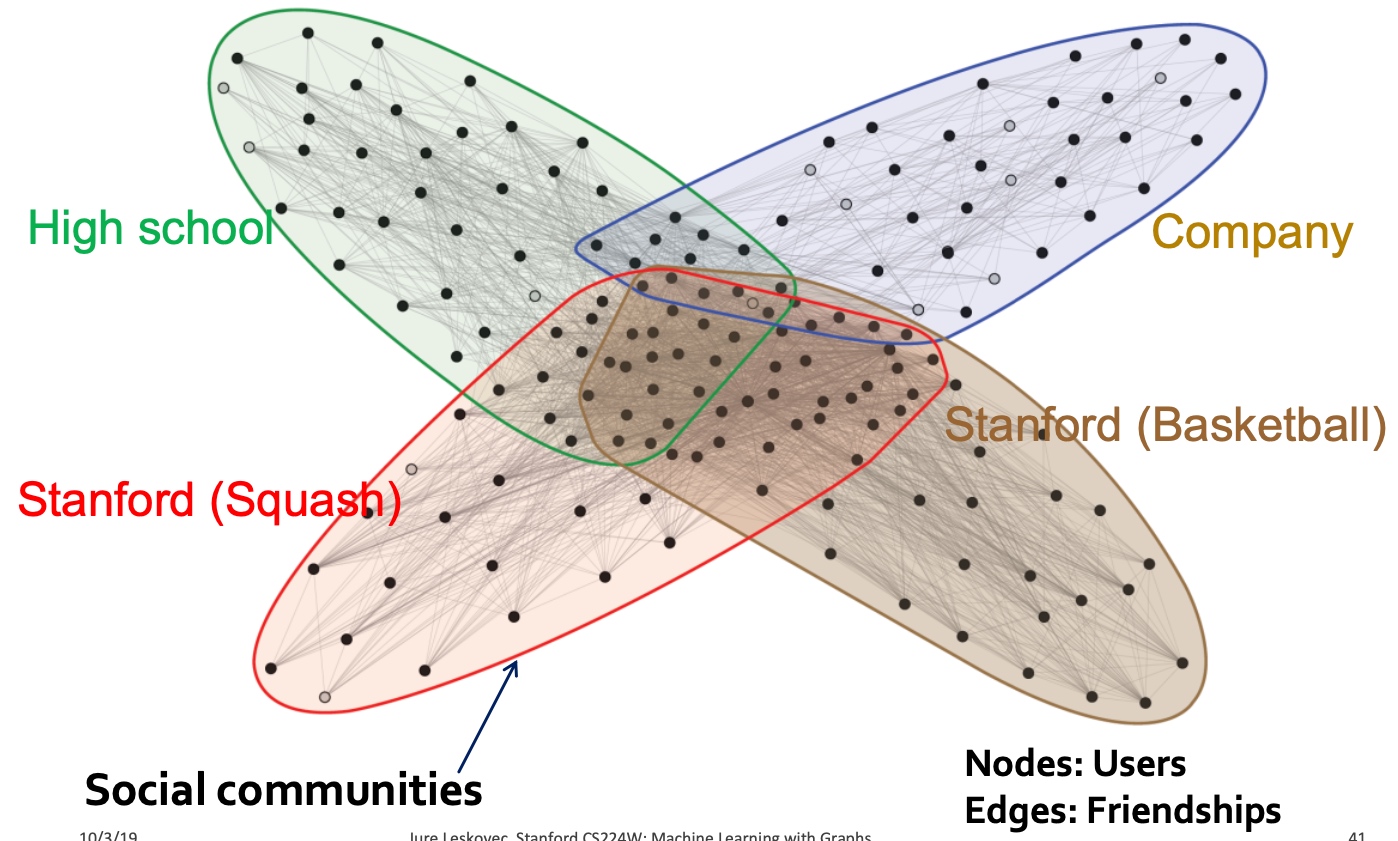
很多实际数据集中,存在有重叠的社群:
facebook的Ego-Network
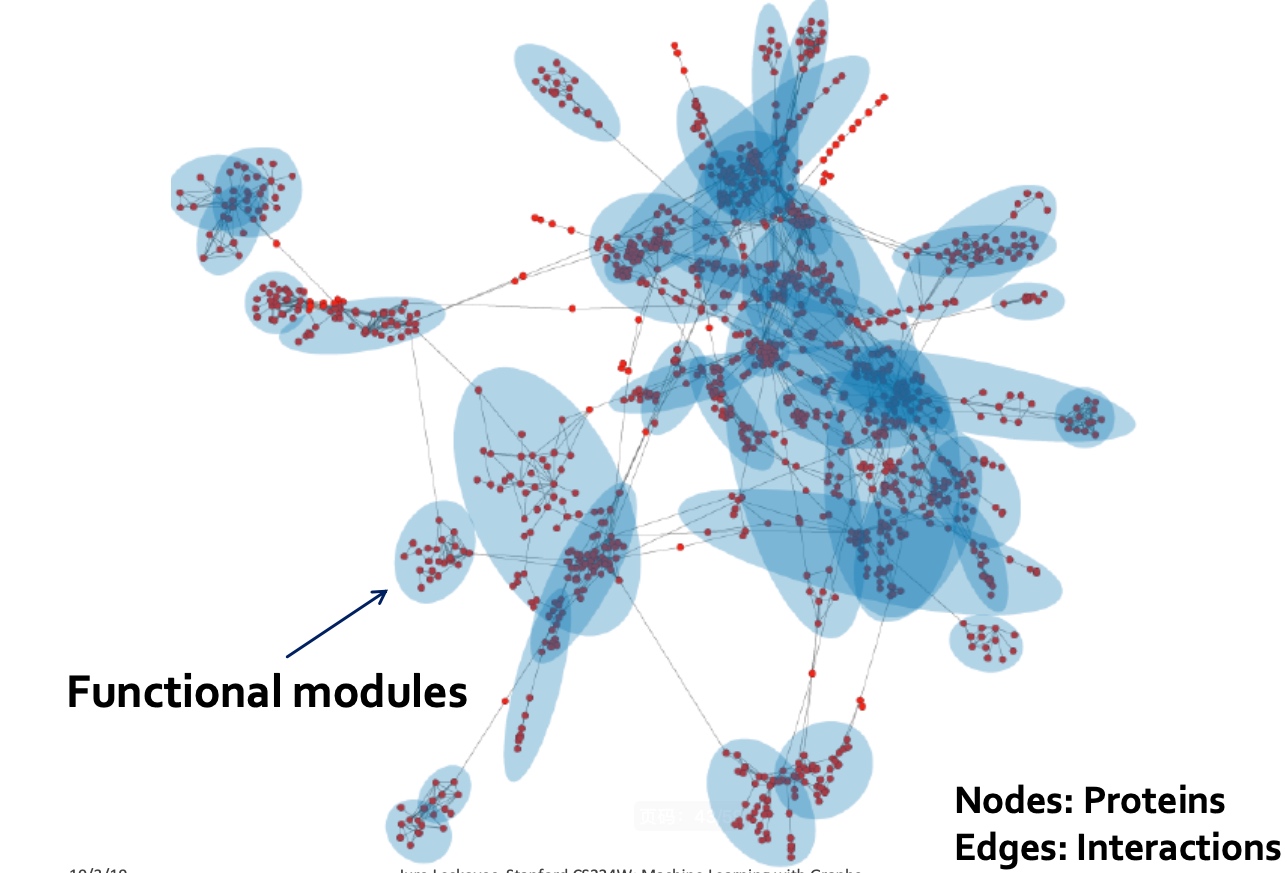
PPI
BigCLAM
BigCLAM主要步骤如下:
- 基于节点所属的社群,构造一个图生成模型,构造方法为AGM(Community Affiliation Graph Model);
- 根据我们实际的图G,假设它是用AGM生成的。寻找一个最优的AGM,能产生我们实际的图G, 通过这个AGM,确定每个节点所属的社区
Community Affiliation Graph Model
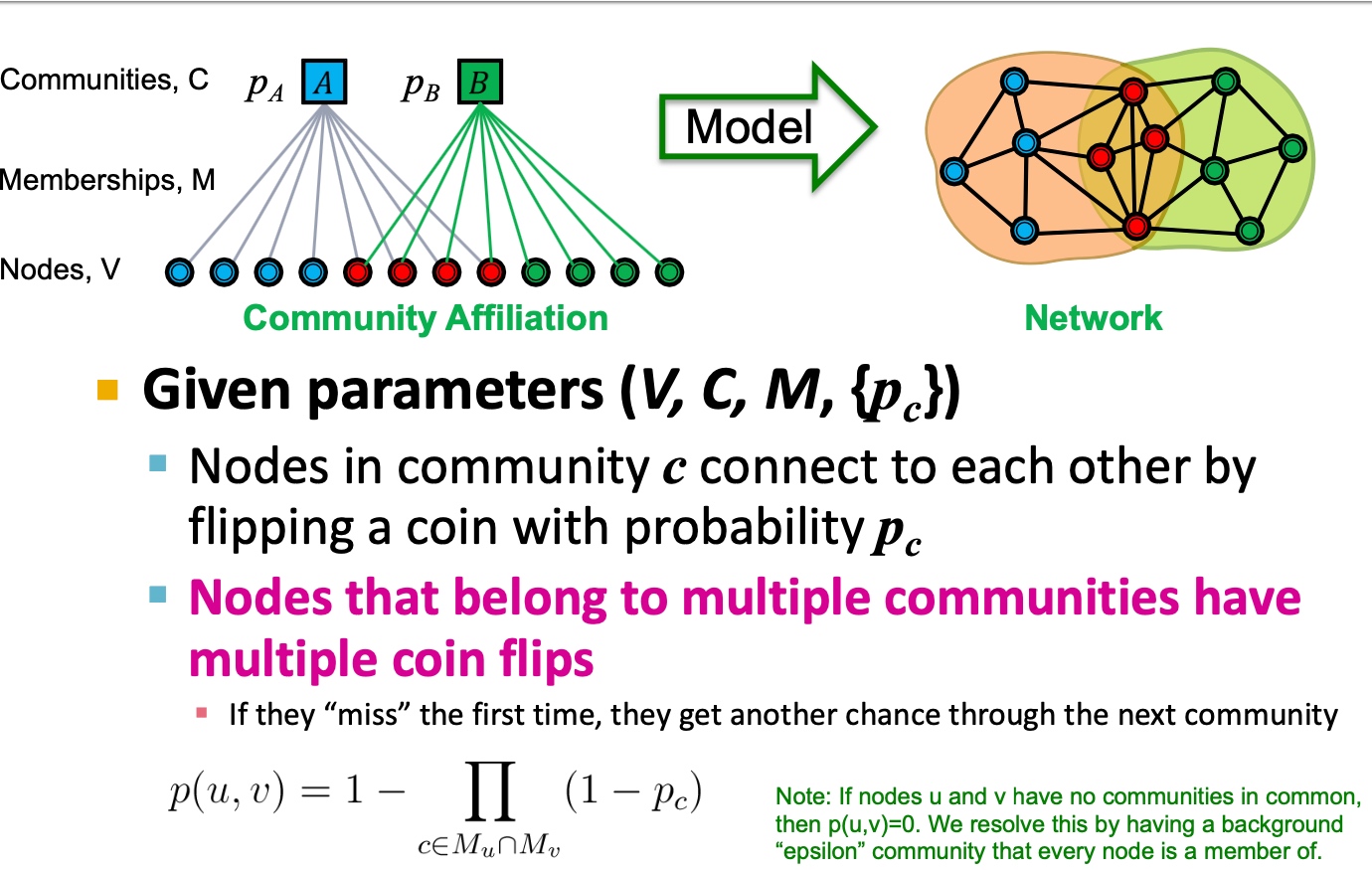
如下图, 左边部分主要包括节点V, 社群C, 从属关系,其中每一个社群的概率为\(p_c\):
- 社群c内的节点,彼此连接形成边的概率是\(p_c\);
- 对于从属与多个社群的节点,如果其在一个社群内没有连接, 其边在另外社群的连接也是可能存在的;
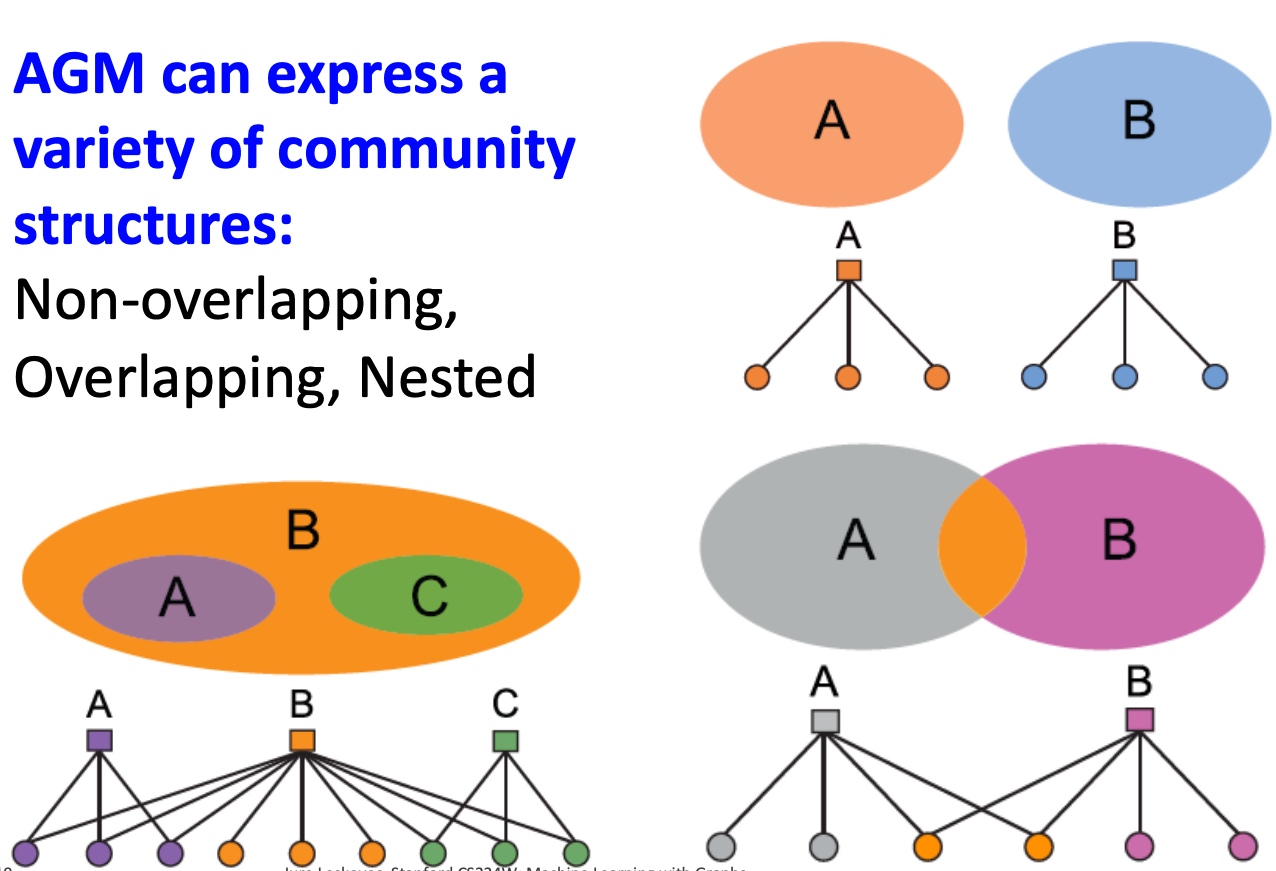
AGM可以生成多种不同的社群结构,如Non-overlapping, Overlapping, Nested:
Detecting Communities with AGM
使用AGM来做社群发现就转换成一个给定graph G, 如何反推AGM的各个参数F:Affiliation Graph M, 社群个数C,以及社群内连接概率\(p_c\)
给定G和F, 计算器似然函数:
\[P(G|F)=\prod_{(u,v) \in G}P(u, v)\prod_{(u,v) \not \in G}(1-p(u,v)) \]上式中前一个连乘表示图当中所有的边的似然函数,后一个表示不在该graph边集合的似然。
考虑到每个节点属于各个社区的权重是不同的, 向量\(F_u\)表示节点u属于各个社群的权重,加上log转换, 所以log似然函数为:
这里和lr的梯度下降很类似,其实就是一样,只需要用梯度下降公司待进去自然就可以算出收敛是的F的参数;
有了F之后, 我们的节点从属社群关系就极其明显了。
总结
今天,课程上主要讲解的是graph中社群的概念,通过Granovetter's theory和真实数据的对比,验证了图当中的强弱连接,从而引出社群概念,然后介绍了一种简单的社群发现算法Louvain Algorithm,通过最大化Modularity Q来保证节点与社群的从属, 最后提供可重叠的社群发现,提出BigCLAM算法,通过最大化log似然函数优化AGM生成对应真实Graph,来得到AGM, 从而得到包括社群从属关系在内的各个参数,从而识别节点从属;